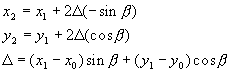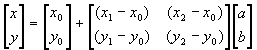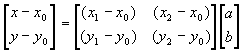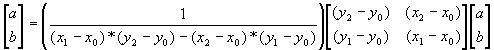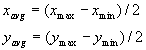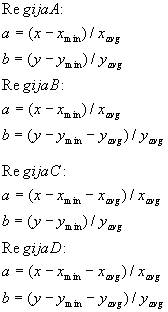Osnovne tehnike
Najprej nekaj besed za lažjo predstavo o zapisu algoritmov
in njihovi implementaciji.Za lažje razumevanje bodo slike v nadaljevanju predstavljene
kot matrike pikslov. Vsak piksel je predstavljen z naravnim številom, ki predstavlja
njegovo barvo. Tudi zapis barv bo omejen na osem bitov (pri črno belih slikah je črna
barva predstavljena s številom 0, bela pa z 255). Ta zapis je tudi najpogostejši v
vsakdanji uporabi. Barvne slike so predstavljene s tremi osnovnimi barvami rdečo, zeleno
in modro. Vsaka osnovna barva pa s prej omenjenimi 256 odtenki. Vse operacije na barvnih
slikah izvajamo na enak način kot na črno belih, sliko predstavimo s tremi matrikami
števil, ki predstavljajo tri osnovne barve.
Aritmetične operacije
Poglavje predstavlja osnovne aritmetične operacije na
slikah, kot so vsota, razlika, množenje in deljenje slik, predstavljene so tudi osnovne
operacije s skalarji. Prav te metode so ena največjih prednosti digitalne fotografije
pred običajno.
Te operacije prestavljajo osnovo za vse kasnejše kompleksnejše
operacije. Vse operacije potekajo na nivoju pikslov, kar pomeni, da številu piksla prve
slike, prištejemo, odštejemo, ..., število, ki si ga lasti istoležni piksel druge
slike.
Vse operacije zahtevajo enake matrike slik, drugače operacije niso
definirane. Pred uporabo opisanih operacij moramo slike normirati (matrike lahko dopolnimo
z maksimalnimi ali minimalnimi vrednostmi – odvisno od operacije, ali pa zmanjšamo
matrike na največje še definirano območje in po operaciji dodamo ostanek).
Vsota slik
Metoda iz niza slik sestavi novo sliko s pomočjo vsote
istoležnih pikslov. Ponavadi poteka na dveh slikah (in postopek po potrebi ponavlja na
novih slikah). Če namesto števil, ki predstavljajo drugo sliko, uporabi skalar, dobi
vsoto s skalarjem. Omejili smo se na 256 barv, problem nastane pri vsotah, ki presegajo
največjo vrednost 255. Najbližja uporabna vrednost je 255, torej vsa števila večja kot
255 zapišemo s tem številom. Nekatere slike lahko postanejo povsem bele, vseeno pa je to
najbližji približek, ki je še uporaben.
Razlika slik

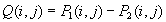
Podobno kot pri vsoti slik sta sliki predstavljeni z
matrikama pikslov. Pri razliki se lahko pojavijo negativna števila, ki so za prikaz
neuporabna. Vsa negativna števila predstavimo z 0 kot najbližjim veljavnim številom.
Množenje slik
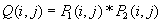
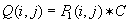
Že osnovno operacijo množenja slik uporabljamo pri detekciji
sprememb gibanja in izboljšavo nekaterih detajlov slik.
Deljenje slik
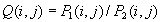
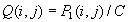
Metoda je primerna za uporabo kot komplement množenju. Pozor velja
predvsem številu 0, oziroma deljenju s tem številom, še posebej, ker se pogosto
pojavlja pri zapisu slik. Deljenje slike same s seboj tudi ni preveč primerno, saj pelje
do velike izgube podatkov.
Linearna kombinacija slik
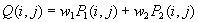
Ta metoda je primerna za izdelavo gladkih prehodov med prikazom dveh
slik in kombiniranjem podatkov iz prve slike s podatki iz druge. K osnovni linearni
kombinaciji lahko dodamo še uteženo linearno kombinacijo, ki se razlikuje po tem, da
vsaki sliki dodamo utež (pomembnost podatkov na določeni sliki). Poseben primer te
metode je interpolacija dveh slik (utež w1 je večja od 0 in manjša od 1):
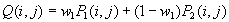
Geometrične transformacije
Osnovne geometrične transformacije predstavljajo osnovo za pozneje
opisani warping in morphing, zato jih predstavljam v posebnem poglavju. Sestavljanje slik
določene scene, ki smo jih posneli pod različnimi koti in z različnimi zamiki zahteva
uporabo transformacij. Med osnovne geometrične transformacije štejemo premik,
povečavo/pomanjšavo (rescaling), zasuk in zrcaljenje.
Premik (translacija) slike
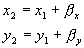
Translacija je najenostavnejša geometrična transformacija. Vsako
točko prestavimo za določeno število pikslov v vertikalni in horizontalni smeri. Kot
vhodni parameter zahteva ta transformacija vektor premika v horizontalni in vertikalni
smeri (bx, by). Uporablja se za iskanje objektov
na slikah, predvsem robov (računalniški vid).
Povečava/pomanjšava slike
Pomanjšava slike temelji na izbiri najprimernejših pikslov. To
lahko opravimo na več načinov. Najenostavnejša metoda je interpolacija pikslov. Pri tej
metodi izberemo območje, ki ga želimo pomanjšati v en sam piksel (dva piksla ali
kvadrat štirih pikslov, izračunamo povprečno vrednost pikslov, ki predstavlja novo
vrednost).
Povečava slike temelji na podobnem načelu, en piksel razvlečemo
na dva ali štiri piksle, ki dobijo isto vrednost kot osnovni. To metodo izboljšamo s
pomočjo interpolacije (sosednjim pikslom priredimo podobne vrednosti).
Zasuk (rotacija) slike
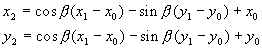
Rotacija predstavlja najtežjo obliko geometričnih transformacij
saj zahteva uporabo interpolacije in kotnih funkcij. Vhodni parameter je predstavljen s
kotom zasuka b in s središčem
rotacije točko (x0, y0). Osnovna enačba ne zadošča popolnoma,
saj v novi sliki pušča luknje. Te luknje bomo zapolnili s pomočjo interpolacije.
Zrcaljenje slike
Zrcaljenje ali preslikavo preko osi delimo na dva enostavna primera
in splošnega:
- Zrcaljenje preko vertikalne osi

- Zrcaljenje preko horizontalne osi
- Zrcaljenje preko poljubne osi
Os je določena s točko (x0, y0) in kotom b . Prva dva primera sta samo posebna primera
tretjega, vendar pa sta zaradi enostavnosti velikokrat uporabljena.
Digitalni filtri
Digitalni filtri so eno najuporabnejših orodij
računalniškega vida in tudi računalniške grafike. Omogočajo izločanje pomembnih
informacij iz slik, izboljšanje kvalitete slik, iskanje objektov na slikah in drugo.
Filtri za izboljšanje kontrasta ter iskanje robov so uporabljeni v
vseh sistemih računalniškega vida, filter povprečja je primeren za umirjanje preostrih
in pregrobih posnetkov in za izločanje šuma.
Digitalni filter je sestavljen iz jedra in popravka. Jedro je
predstavljeno s kvadratno matriko, popravek pa vsaj približa vsoto nazaj k začetni,
drugače bi večkratna uporaba filtra popolnoma izbrisala vsebino slike (popolnoma
počrnila ali pobelila).
Velikost matrike je zelo pomembna, velike matrike zahtevajo visoko
časovno kompleksnost izračunavanja novih vrednosti, omogočajo pa bolj natančno uporabo
filtra. Najpogosteje uporabljeni so filtri z jedrom matriko 3x3.
Konvolucija
Konvolucija, čeprav zveni zelo zapleteno, je v resnici zelo
preprosta. Vrednost določenega piksla določamo s pomočjo vrednosti njegovih sosedov.
Vsak sosed doda določeno vrednost, odvisno od lastne vrednosti in uteži, ki jo določa
matrika jedra filtra. Našo matriko jedra filtra polagamo po začetni sliki, izračunane
vrednosti, popravljene za vrednost popravka (izračunano vrednost delimo z vrednostjo
popravka), pa se zapiše v novo sliko.
Na robu slike dobimo območje, ki ga filter ne doseže, tako
imenovani robni problem.Ta problem rešujemo na več načinov. Najpreprostejši način je,
da ta okvir enostavno pozabimo. Lahko prepišemo vsebino osnovne slike ali pa naredimo
interpolacijo med vrednostmi stare slike in robnimi vrednostmi nove slike (ta način še
najmanj popači sliko, zahteva pa nekaj dodatnega programiranja). Velikost stranice
matrike jedra filtra pri konvoluciji mora biti liha, ni pa nujno, da je matrika kvadratna
(uporabljamo matrike velikosti 3x3, 3x5, 5x5, ...).
| Vpiši koeficiente matrike jedra (prvih devet okenc) in vrednost popravka
(zadnje okence): |
|
Enotski filter
Ta filter ne naredi ničesar, predstavljen je samo kot zanimivost,
kaže pa način delovanja filtra.
Popravek je 1 (brez popravka).
Nizko prepustni filtri (Low pass spatial
filters)
Filtri te skupine prepuščajo komponente nizkih frekvenc, visoke pa
porežejo. Takšni filtri se uporabljajo za odstranjevanje šuma velikosti en ali dva
piksla (tak šum je skrit v visokih frekvencah). Vsota vrednosti sosedov pomnožena z
utežmi filtra je normirana s pomočjo popravka (vsota uteži normirana s popravkom je
enaka 1). Meja prepustnosti je določena z velikostjo matrike jedra in s koeficienti te
matrike. Kako delujejo takšni filtri? Ko s filtrom prehajamo po delu slike, kjer so
spremembe med sosednjimi piksli majhne (nebo, enotna površina, ...), vrača filter skoraj
enake vrednosti. Pri prehodu čez področje, kjer so spremembe med sosednjimi piksli
velike, pa filter zamaže (izračuna povprečje sosednjih pikslov). Slike, ki smo jih
obdelali s takšnim filtrom, so nekoliko zamegljene in nežnejših robov.
Nekaj primerov nizko prepustnih filtrov:
| Povprečje
Popravek 9
|
LP2
Popravek 10
|
LP2
Popravek 12
|
Gaussov
Popravek 16
|
Visoko prepustni filtri (High pass
spatial filters)
Poudarjajo visokofrekvenčne komponente slike. Omogočajo enostavno
razpoznavanje in poudarjanje objektov na sliki (poudarjajo spremembe na sliki). Paziti
moramo na šum, ki ga tudi Poudarjajo (nizko prepustni ga odstranijo, visoko prepustni pa
poudarijo). Ponavadi imajo ti filtri velike središčne vrednosti matrik jedra (srednja
vrednost v matriki je velika). Vrednost piksla na področju velikih sprememb na sliki je
pomnožena z srednjim elementom, ki je pri visoko prepustnem filtru velik. Tako se
pomnoži vrednost piksla z velikim številom, sosedje pa manj vplivajo na vrednost novega
piksla. Tako se poudarijo nagle spremembe na sliki, ki ustrezajo robovom objektov. Nekaj
primerov visoko prepustnih filtrov:
Mean removal
| -1 |
-1 |
-1 |
| -1 |
9 |
-1 |
| -1 |
-1 |
-1 |
Popravek 1 |
HP1
Popravek 1 |
HP2
Popravek 1 |
HP3
Popravek 16 |
Detekcija robov
Detekcija robov je prva naloga vsakega sistema za
računalniški vid. S pomočjo filtrov za detekcijo robov spremenimo sliko v obrobe
objektov, vse ravne površine postanejo črne. Takšna slika je primerna za nadaljnje
razpoznavanje, saj so objekti natančno določljivi. Filtre te skupine pa lahko
uporabljamo tudi v drugačne namene, na neki sliki lahko samo poudarimo robove objektov za
večjo preglednost. Vsota uteži matrike jedra filtra je enaka 0, kar pomeni, da bo slika
postala temnejša. Samo velike razlike (visokofrekvenčne komponente) bo takšen filter
prepustil, enotne površine pa bo odstranil (postale bodo črne). Nekateri filtri
poudarjajo samo robove, ki se širijo v določeni smeri, vse ostale pa zabrišejo. Tako
moramo uporabiti filtre za vse želene smeri in sestaviti skupno sliko.
Laplaceov filter
Kot poseben primer filtra za detekcijo robov si oglejmo Laplaceov
filter, ki je najbolj poznan. Ta filter poudarja robove v vseh smereh, torej zahteva samo
en prehod slike. Filter temelji na matematičnih osnovah:
Laplaceova transformacija funkcije f(x,y) je:
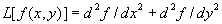
Za diskretno funkcijo (naša funkcija je diskretna, saj uporabljamo
cele vrednosti za piksle) lahko aproksimiramo:

Torej lahko aproksimiramo Laplaceovo transformacijo z:

Predstavimo z matriko jedra filtra:
Veekrat se uporablja zapis Laplaceovega filtra v spodnji obliki,
samo predznaki so spremenjeni:
| -0 |
-1 |
-0 |
| -1 |
4 |
-1 |
| -0 |
-1 |
-0 |
Nelinearni filtri
Filtri za detekcijo robov poudarijo robove objektov, poudarijo pa
tudi šum. Ta šum ne moremo odstraniti z opisanimi filtri brez izgub koristnih podatkov
(nizko prepustni filtri bi zabrisali robove). Uporabimo filtre, ki temeljijo na
statistični teoriji, najbolj poznan in najlažji za implementacijo je mediana. Namesto
uteževanja vrednosti sosednih pikslov, tako delujejo vsi linearni filtri, mediana sortira
sosede po velikosti in določi srednji element. Ta vrednost je nova vrednost obiskanega
piksla. Kako deluje ta filter? Če vrednost piksla dosti odstopa od njegovih sosedov lahko
z veliko verjetnostjo trdimo, da je ta piksel šum in ga lahko odstranimo (namesto njegove
vrednosti zapišemo vrednost soseda, ki ima srednjo vrednost). Pri uporabi tega filtra pa
moramo biti previdni, saj odstrani tudi robove, ki so široki samo en ali dva piksla.
Zahtevnejše tehnike
Med zahtevnejše metode računalniške grafike uvrščamo vse
sestavljene transformacije. Pogosto so te metode časovno in prostorsko potratne. Do sedaj
so bile le redko uporabljane, z razvojem računalniške strojne opreme pa si vedno bolj
utirajo pot v naš vsakdan. Predstavil bom dve metodi, ukrivljanje in preoblikovanje, ki
sta najbolj raziskani in obdelani obenem pa mnogim popolnoma nepoznani. Posebej
matematične teorije na katerih slonita ti dve metodi so precej zapletene. Obstaja
množica različnih implementacij.
Warping
Geometrično ukrivljanje, kot bi lahko prevedli angleško
besedico ukrivljanje, pogosto opazimo v novejših filmih in reklamah. Še do pred kratkim
je bila potrebna že za enostavne primere posebna strojna oprema (zelo hitri
računalniki), saj je metoda časovno zelo potratna. Ukrivljanje bi najlaže predstavili s
primerjavo s koščkom gume na katerega narišemo določen objekt. Ko gumo zvijamo, se
zvija tudi objekt in nastajajo ukrivljene podobe (warped images). S premikom točke na
sliki uporabnik poda računalniškemu algoritmu za ukrivljenje parameter, s katerim
izračuna spremenjeno sliko. Točke v bližnji okolici se premikajo skupaj s kontrolno
točko (premiki točk so uteženi z oddaljenostjo od kontrolne točke). Tako ukrivljenje s
pomočjo ene kontrolne točke ne vpliva na celo sliko ampak samo na bližnjo okolico
kontrolne točke. Po potrebi izberemo nove kontrolne točke na obdelani sliki in
nadaljujemo z ukrivljenjem.
Poglejmo še matematično teorijo, ki sloni v ozadju metode:
Dva koordinatna sistema vhodni V(u,v), v katerem se nahaja izvorna
slika in izhodni I(x,y), ki vsebuje novo sliko. Tako lahko definiramo funkcijo ukrivljenja
z dvema funkcijama Wx(u,v), Wy(u,v), ki določata izhodni
koordinatni sistem za vsako točko (u,v). Inverzni funkciji ukrivljenja določimo kot IWu(x,y),
IWv(x,y), ki določata vhodni koordinatni sistem.
Te funkcije določajo transformacijo med obema sistemoma, poleg lege
kontrolnih točk določata tudi lego okoliških točk. Če se vrnemo na primer s koškom
gume, potem te funkcije določajo kako se bo zvijala in širila guma.
Seveda pa naše funkcije ne bodo tako komplicirane kot so funkcije,
ki definirajo obnašanje gume. Primitivnejši model popolnoma zadošča, popoln model bi
bil tudi časovno preveč potraten. Pravokotnik ali paralelogram je enostavno določiti z
afinimi transformacijami, bilinearno preslikavo bomo uporabili za določanje štirikotnih
območij. Z afinimi preslikavami lahko vsaki točki, ki pripada območju omejenem z
določenim paralelogramom, lahko določimo parametre (koordinate), ki nam omogočajo
enostavno in enolično določitev te točke.
Enačba zapisana v matrični obliki za določitev koordinat točke:
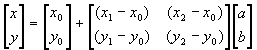
Prevedemo na inverzno enačbo (v dveh korakih):
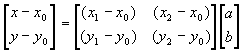
Končna rešitev:
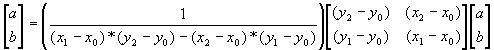
V poljubnem štirikotniku (območju omejenem s štirikotnikom) lahko
določimo poljubni točki koordinate s pomočjo bilinearne preslikave. Štirikotnik je
omejen s premicami p1, p2, p3, p4, lahko
določimo točki e1, e2 na robovih štirikotnika:
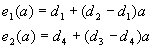
S pomočjo teh dveh točk določimo položaj (koordinate) naše
točke p:
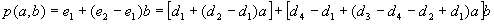
Poenostavljeno:
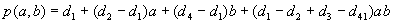
Zadnjo enačbo imenujemo tudi bilinearna transformacija, p je
določena z dvema linearnima interpolacijama. Ta enačba je posplošitev prejšnje enačbe
za afine preslikave.
Temelje za metodo smo postavili, sedaj pa se lotimo ukrivljanja.
Sedaj znamo določiti koordinate točkam v območjih omejenih s pravokotniki in
paralelogrami (prvi dve enačbi – afine transformacije) in v območjih omejenih s
štirikotniki (tretja enačba – bilinearna transformacija).
Program naj bi deloval po naslednjem receptu: Najprej določi mrežo
možnih kontrolnih točk (če bi upoštevali vsak piksel kot možno kontrolno točko, bi
bil program prepočasen), uporabnik z miško izbere kontrolno točko, program določi
okolico te točke (zaplato). Ta zaplata ki je omejena s pravokotnikom, ki se bo
spreminjala med izvajanjem algoritma. Uporabnik nato premakne izbrano točko na novo
lokacijo v območju izbrane zaplate in s tem požene preslikovalnik. Program premakne
točke zaplate tako, da kontrolna točka ponovno preide v središče zaplate.
Program deluje tako, da iz štirih vhodnih štirikotnikov, v štiri
izhodne pravokotnike. Ko uporabnik premakne kontrolno točko v zaplato pripravljeno za
ukrivljanje, program razdeli to zaplato na štiri štirikotnike. Po opravljeni
transformaciji se kontrolna točka ponovno vrne v izhodiščni položaj na sredino
zaplate, tako da deli zaplato na štiri enake pravokotnike. Prevedbo iz vhodnih
štirikotnikov v izhodne pravokotnike uporabljamo, ker lahko z njihovo pomočjo
naslavljamo točke na vhodni in izhodni sliki, točke z istim naslovom dobijo isto barvo.
Afina transformacija prvih dveh opisanih enačb nam omogoča naslavljanje izhodnega
pravokotnika, pri tem parametra a in b zavzemata vrednosti med 0 in 1. Bilinearna
transformacija pa omogoča naslavljanje točk v vhodnem štirikotniku (parametra a in b
zavzemata enake sta tudi tukaj med 0 in 1). Obe preslikavi določata vse točke v
omenjenih območjih. Točkam, ki imajo enake vrednosti a in b, priredimo enako barvo (na
primer: imamo vhodno točko z vrednostma a=0.5 in b=0.7 in barvo 200, izhodna točka z
enakima vrednostma a in b dobi barvo 200).
Obstajata dva načina za ukrivljanje slike vnaprejšnje določanje
vrednosti pikslov (forward maping) in vzvratno določanje vrednosti pikslov (inverse
maping). Pri prvem načinu se sprehodimo po vseh pikslih vhodne slike (u,v) in zapišemo
njihove barvne vrednosti na piksle izhodne slike z enakimi vrednostmi parametrov
(koordinat) a in b. Pri vzvratnem določanju pa se sprehajamo prek izhodnih pikslov (x,y)
in iščemo barvo pikslov na vhodni sliki z enakimi koordinatami. Določen piksel na
izhodni sliki ne ustreza samo enemu pikslu vhodne slike in obratno, zato pregledujemo
celotno sliko in ne samo en piksel. Pri razširjanju slike dobi barvo enega samega
vhodnega piksla več izhodnih, pri ožanju pa več vhodnih pikslov določa barvo enega
samega izhodnega. Pri vnaprejšnjem določanju lahko dobimo luknje v izhodni sliki (zaradi
opisanih pojavov), lahko jih rešujemo z interpolacijo ali na bolj zapletene načine. Pri
vzvratnem določanju pa do teh lukenj ne pridem saj določamo barvo vsakega izhodnega
piksla, lahko pa pride do določenih popačenj. Zaradi hitrosti in enostavnosti se bomo
omejili na vzvratno metodo.
- Zaplato ukrivljenja določamo z zaslonskimi koordinatami xmax,
ymax v spodnjem desnem kotu in xmin, ymin v zgornjem
levem kotu.
- Točka K (xctrl, yctrl) je kontrolna točka na
zaslonu.
- Točka A (xavg, yavg) predstavlja sredinsko
točko zaplate:
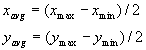
Enačbi afine preslikave lahko poenostavimo, ker je naša zaplata
pravokotna in poravnana z osmi zaslona, tako afine preslikave predstavimo z enostavnimi
enačbami (parametra a in b sta poravnana z x in y osma in ju samo normaliziramo):
Zaplato razdelimo na štiri pravokotnike in jih označimo z ABCD v
obratni smeri urinega kazalca.
Vrednosti, ki jih dobimo s temi enačbami vstavimo v tretjo enaebo
(enaeba bilinearne preslikave) in dobimo koordinate vhodnega piksla. Tudi enaebo
bilinearne preslikave lahko poenostavimo, ker so štirikotniki skoraj pravokotni
(premaknjena je le ena kotna točka - kontrolna točka). Poenostavljene enačbe bilinearne
preslikave:

Program za vsak izhodni piksel poišče vrednosti a in b s pomoejo
prvega sklopa enačb, nato uporabi drugi sklop enačb s parametroma a in b. Tako doloei
koordinate pripadajoče točke na vhodni sliki (koordinate so realna števila, uporabimo
zaokrožanje, saj vemo da so koordinate pikslov na sliki cela števila). Barva vhodnega
piksla z izračunanimi koordinatami je nova barva izhodnega piksla. Program na koncu
metode prepiše sliko iz izhodne v vhodno in tako omogoei novo izbiro kontrolne točke.
Seveda pa je predstavljena metoda poenostavljena, lahko bi uporabili polinome višje
stopnje v enačbah in tako pridobili na natančnosti (uporabili bi vee kontrolnih toek),
zavedati pa se moramo, da je že ta osnovna metoda časovno požrešna.
Morphing
Ta metoda je pravzaprav samo nadaljevanje prej opisane metode
ukrivljanja. Preoblikovanje zahteva dvakratno ukrivljanje z interpolacijo po zlepkih
(spline interpolation) med začetno in končno sliko. Pred opisom podrobnosti si oglejmo
uporabo metode. Preoblikovanje je proces pri katerem generiramo vmesne slike med začetno
in končno sliko. Število vmesnih slik ni omejeno, čim večje je, bolj mehko in neopazno
bo prehajanje. Na začetni in končni sliki izberemo pomembne točke (ponavadi uporabljamo
metodo nad dvema obrazoma, pomembne točke so torej oči, nos, usta).
Kako natančno določamo te točke je odvisno od implementacije same
metode, čim več je ključnih točk, bolj natančno bo program generiral vmesne slike,
potreboval pa bo več časa. Začetno sliko spremenimo v končno in končno v začetno (v
začetku zapisano dvakratno ukrivljanje).
Primer: avto krivimo prek več slik (postopoma izvajamo ukrivljanje)
v tovornjak, tako da se ključne točke čimbolj ujemajo (luči, kolesa, robovi...), enako
storimo tudi s tovornjakom. Izračunamo uteženo povprečje soležnih slik in naredimo
interpolacijo barv med soležnimi slikami.
Majhne skrivnosti
velikih mojstrov programiranja
Kot dodatek poznanim in velikokrat uporabljenim tehnikam
si oglejmo še nekaj grafičnih algoritmov. Te tehnike ne sodijo med osnovne metode
obdelovanja digitalnih slik. Njihova implementacija je enostavna saj za programsko
implementacijo algoritmov ni potrebno znanje teorije na kateri temeljijo. Večina teh
tehnik je manj znanih in tudi redko uporabljenih, enostavnost uporabe in zadovoljivi
rezultati pa jih uvrščajo v ta učbenik.
3D efekt graviranja na 2D
sliki
Če si predstavljamo sliko kot 3D ploskev, lahko uporabimo
standardne tehnike 3D senčenja. Senčenje je precej požrešna operacija, tudi če
upoštevamo samo en izvir svetlobe, v tem primeru pa lahko upoštevamo znane omejitve
ploskve in algoritem zelo pohitrimo. Kot izvorno sliko lahko uporabimo poljubno umetnino
ali fotografijo, zavedati pa se moramo, da bodo pregost relief ali pa slabo definirani
prehodi zelo zameglili ciljno sliko.
Izvorno sliko si moramo predstavljati v treh dimenzijah.
Tako lahko definiramo normalni vektor, ki nam bo predstavljal temelj za naše izračune
odboja navidezne svetlobe.
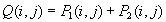
Zaradi lažje razlage se bomo ponovno omejili na samo en
izvor svetlobe.
Enostavna formula senčenja:
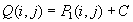
Rezultat senčenja predstavlja sivinsko sliko, enostavno
množenje z izbrano teksturo pa omogoča uporabo na poljubni sliki.
Zanimiv je odziv ljudi na tako predelane slike. Če
izberemo izvor svetlobe iz gornjega roba slike, večina ljudi predmet opazi kot izbočen,
položen na samo sliko. Prestavitev izvora svetlobe na spodnji rob slike postavi predmet v
samo sliko, gravura.
Metoda je nedefinirana za sam rob slike, problem rešujemo
podobno kot pri uporabi filtrov. Lahko enostavno prepišemo točke z izvorne slike,
zmanjšamo velikost ciljne slike za rob, uporabimo interpolacijo točk ali kakšno bolj
zapletenih metod. Avtorji metode prepuščajo uporabnikom implementacijo rešitve.Metoda
uporablja masko velikosti 3x3, upoštevati moramo rahlo razmazanje slike, popravimo lahko
z enim od filtrov za ostrenje slike.
Transformacije posameznih
pikslov
Veliko uporabnih metod za izboljšavo slik temelji na
enostavnih transformacijah vrednosti posameznih pikslov. Nova vrednost posameznega piksla
je odvisna samo od stare vrednosti, tako imenovana ena na ena transformacija. Enostavne
različice teh metod delujejo na sivinskih slikah, omejili se bomo samo na takšne slike,
tudi obseg sivin bomo zaradi lažje razlage omejili na 0..255. Število 0 predstavlja
črno barvo, 255 pa belo, vmesne vrednosti pa sivine.
Barvno paleto preslikamo v interval realnih števil med 0
in 1. Tako lahko izrišemo graf funkcije. Najenostavnejša je identična preslikava:

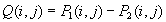
Ta preslikava ne povzroči nobene razlike. Uporabnejša
metoda je kvantizacija. Interval razdelimo na izbrane dele, vse vrednosti določenega dela
preslikamo v eno samo vrednost. Tako dobimo stopničasto krivuljo, prikazano na drugem
grafu.
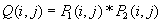
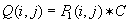
Kontrast slike spreminjamo s strmino krivulje funkcije f(x).
Bolj strma krivulja pomeni večji kontrast in obratno. Ponavadi je dobimo najboljše
rezultate izboljšanja kontrasta na sliki s postavitvijo mejnih vrednosti. Vse vrednosti
pod spodnjo mejno vrednostjo in vse vrednosti nad zgornjo mejno vrednostjo postavimo na 0.
Vmesne vrednosti pa prilagodimo strmejši transformacijski krivulji.
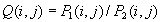
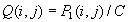
Splošno svetlost slike spreminjamo s tako imenovanim
GAMMA popravkom.To je nelinearna transformacija, njen rezultat pa je primerljiv za
nastavitvijo svetlosti na običajnih televizijskih ekranih.
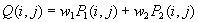
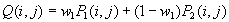
Od vrednosti parametra GAMMA je odvisna velikost in tudi
smer spremembe. Vrednost večja kot 1 sliko osvetli, vrednost med 0 in 1 pa potemni.
Seveda vrednost parametra GAMMA enaka 1 ne povzroči nobene spremembe.
Učbenik spisal v okviru diplomske naloge Jernej Vičič.